淺談測不準原理
測不準原理一直是困擾著許多高中生的物理理論,大部分人的詮釋常常會缺臨門一腳,使得回去思考後很難自圓其說。剛好最近閒暇之餘在幫忙準備明年BioPhyChem的物理組教材,決定趁這個機會來寫一篇通俗(適合稍微有點基礎的高中生)的測不準原理介紹。
要提測不準原理,得先帶點時代背景,了解這個理論產生背後的來龍去脈。首先是在1905年,愛因斯坦(Einstein)推測光波具有粒子性,將馬克斯威爾(Maxwell)電磁波方程中的角頻率和波向量乘上約化普朗克常數得到光子的能量與動量,並以此發展出光子論。1923年德布羅伊(de Broglie)為了解釋波爾(Bohr)在氫原子模型中所給的穩定態條件而發表了物質波理論,提出任何粒子都具有波動性的假設。如果物質可以視為波,自然就一定會滿足一個相應的波動方程,對應到物質就被稱作物質波方程。這個物質波方程在不久後被薛丁格(Schrodinger)透過非相對論性能量動量關係式給湊出來了,以下為簡略的推導:
(1)將能量動量關係式列出,並透過物質波的假設將其轉換成頻率和波向量的型式。
(2)將物質波方程的波函數先做傅立葉展開,並把能量動量關係式乘進去得到零。
物理學家得知了粒子具有波動性,並推出了物質波方程,但此時大家仍不清楚物質的波動性究竟有甚麼樣的含意。薛丁格方程被推出來的不久後,另一位物理學家波恩(Max Born)證實了波函數對自己內積即是粒子存在位置的體機率密度。(為求寫作方便我接下來一率將機率密度稱作機率,除非描述的性質跟密度有絕對關聯才會另行強調。)
在古典物理中,只要有足夠的條件,就能透過物理定律完全推測出未來將發生的事情,像是高中所學的:在真空中有均勻重力場的地方,給物體一個初速和一個仰角,你就能算出接下來物體的軌跡會是拋物線。然而在量子力學的世界,粒子的行為描述是由機率構成的。什麼是「由機率構成」呢?Dirac的解釋是:我們沒辦法100%完全精確預測出物體在t時刻後的位置和動量,只能掌握在t時刻後物體存在於某段位置的機率以及物體擁有某動量的機率。
舉一個運動中的粒子來說,我能透過粒子的物質波函數內積得到一個機率分佈,這個機率分佈告訴我粒子五秒後位於x=5m~x=6m的機率是60%,粒子的動量介於3kg*m/s~8kg*m/s的機率是40%。也就是說,給定一個粒子完全相同的起始條件,它接下來的行為有無限種不同可能,每種可能都會對應到一個機率,這樣的機率分佈即是由波函數自己內積求得。這件事情等同於告訴我們,不論你條件再怎麼充裕,你只能透過這些條件來預測未來發生某事件的機率,但沒辦法百分之百確定到底會發生甚麼。於是,人類想完全成為神的夢想,被量子力學給擊垮了。
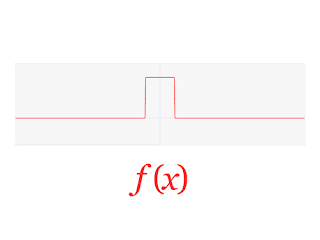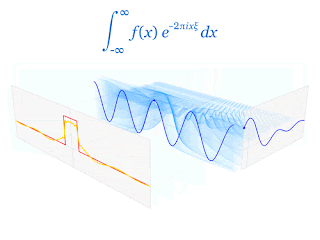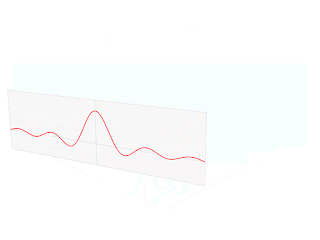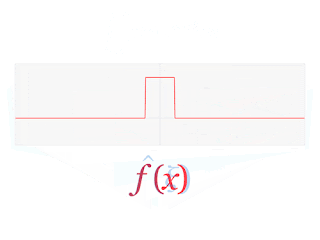
在正式進入測不準原理前,除了波函數外還需要先知道傅立葉轉換(Fourier transform)。傅立葉轉換是一種可以將任何函數拆解成無限個單頻波疊加的數學工具,其中單頻波的頻率組成是連續的,且每種單頻波都會對應到一個權重值,使得全部的單頻波以這樣的權重疊加起來可以得到原函數。以下面這張圖為例子,你可以清楚看到一個方形脈衝的傅立葉轉換疊加型式。
讓我們來考慮一個一維粒子的問題:設定某一維粒子起始的位置機率分佈為高斯常態分佈。因為粒子有波動性,所以粒子的波函數也可以進行傅立葉轉換,得到對應的單頻波組成權重函數。這些單頻波中的波向量項在德布羅伊的理論下對應到的即是粒子的動量,所以將它的權重函數自己內積(也就是取絕對值平方)對應到的便是動量存在的機率密度分佈(這件事情較嚴謹的論證需要引用到數學上的Parserval定理,可知道轉換前後的波函數皆為歸一函數)。若將這個高斯分佈做傅立葉轉換,得到的波向量權重函數絕對值平方(也就是動量的機率密度分佈)如下:
我們亦可以再將這個波向量的權重波函數進行傅立葉反轉換並引入時間項,再取平方得到機率密度對應位置-時間的函數關係如下,它顯示了任一時刻粒子存在任意位置的機率密度:
現在讓我們粗略的定義一下不准量。假設我在粒子位置的機率分佈內選取一個區間,指定粒子位置存在這個區間的機率是P,接著把這個區間可能有的最小寬度稱做位置的不準量。在動量的機率分佈上,會出現一個相應的動量區間,粒子擁有的動量存在這個動量區間的機率也是P,而此時這個區間的寬度則稱做動量的不準量。
數學上的本質顯示,原本的機率分佈和傅立葉轉換後相應的動量分佈的不準量增幅趨勢是相反的,且不論位置的不準量是多少,最後所得到的位置和動量的不準量乘積一定會大於特定值。也就是當原本的位置機率函數不準量愈低時,轉換後得到的動量機率函數的不準量一定會愈高。這個現象是波的本質,在數學上稱做對偶轉換,而位置與動量互為對偶空間。測不準原理之所以會成立,是因為粒子被證實有波動性,波的對偶本質使得動量和位置的不準度乘積受到限制。
在一般情況中,選取的區間是以峰值為中心向左右展開一個標準差(由峰值展開可使對應原指定機率所得到的區間寬度最低),因而位置不準量是原機率分佈的一個標準差的大小,並將同樣的不準量定義用在波向量分布上(一個標準差)。以高斯常態分佈的例子來看,在這樣的不準量定義下,起始時的位置和波向量之不準量互為倒數,於是會滿足下式:
將波向量轉換成動量就會變成下式:
由前面推得的機率密度對應位置-時間的函數可知,隨著時間在增加,其機率分佈的標準差會上升,位置的不準量也會跟著上升,因此對所有時刻的情況來說,位置和動量的不準量乘積就會變成常見的測不準原理型式:
稍微強調一下,由於不準量是人為定義的,所以位置和動量不準量乘積的下限是不定的,一切都由最初的不準量定義來決定。今天如果我把不準量定義成1.5個標準差,下限就會跟著變。不過對測不準原理來說,重點不在於不準量的乘積下限是多少,而在於兩者的乘積有「下限」且不可能等於零。無法同時確切預測位置和動量的精確值,才是測不準原理的精神。除了本質的意涵外,在應用上,多粒子系統的薛丁格方程很難得到精確解,但使用測不準原理卻能計算薛丁格方程的良好近似解,也可以用來在某種程度上估計出一些系統的基態能量,這也是它這麼被看重的原因之一。
現在讓我給一個思想實驗來加深對測不準原理的理解。假想有1000萬個一樣的盒子,每個盒子裡面都裝著一模一樣的物體。每個盒子旁各站一個人,在同一個時間讓這1000萬個人把面前的盒子打開,並且「測量」他們所看到的「物體位置」。這邊先假設這些人測量位置的技術能達到完美,晚點再討論不完美的情況。
因為物體的位置在盒子被打開前僅是一種機率分布,所以即使初始條件相同(一樣的盒子,一樣的物體,同時打開),打開盒子後每個人看到的物體的位置都不太一樣:假設看到物體位於x1的人有a1個,物體位於x2的人有a2個......依此類推,接著我們可以做出一張分布圖,橫軸是物體的位置x,縱軸是看到物體位在x的人數a,當我們把1000萬人推廣到無限人,這張分布圖便是物體的位置機率分佈。
用相同的方法,如果我們在讓這1000萬個人把面前的盒子打開的同時,請他們「測量」的是他們所看到的「物體動量」,便可以得到物體的動量機率分佈。最神奇的事情發生了:你將會發現,這兩個機率分佈的原波函數互為對方的傅立葉變換。量子力學是正確的!
值得注意的一點是,我們得到的這兩組機率分佈,是在盒子被「打開」之前,物體的位置和動量的機率分佈。因為在打開之前,大家都不知道盒子裡面物體的型態可能是甚麼,於是我們會有一個期望可能看見的機率分布(起始的波函數平方),也就是剛剛被那一千萬個人所統計出來的那兩張分布圖。然而當盒子被打開時,假設你讓這些人測量位置,使得位置被「精確量測」,這些人看到的位置波函數機率分佈會變成Dirac delta Function(你只要知道這是一種寬度零高度無限的尖尖的函數就可以了),位置波函數的不準量變成零(因為已經假設測量是完美的)。為了不違反測不準原理,傅立葉轉換後物體的動量波函數的不準量變成無限大。

事實上這個時候,你的等效外加位能包含了「黃衣人測量位置的外加位能」與「黑衣人測量動量的外加位能」,因此把這兩個位能疊加後考慮進薛丁格方程裡頭,最後得到的波函數就無法在動量和位置上都成為Dirac delta Function,而是都有些胖胖的,不準量分別是Δx和Δp,物體在此時就會同時擁有很多位置和很多動量。如果Δx和Δp很小的話,一般人肉眼分辨不出這些不同位置及不同動量的微小差異,因而會自動把位置波函數和動量波函數的期望值看作是位置和動量的精確值。但如果Δx和Δp很大的話,你所看到的物體位置可能就會變得糊成一團、物體動量則好像同時用一堆不同方向不同大小的速度晃動,這就是許多量子力學科普書很愛描述的量子微觀現象。
關於測不準原理物理意義的詮釋就到這邊,我要回過頭來給出一個波函數「準」的程度的數學定義。回到高斯機率分佈函數的例子:我不要求位置的測量「絕對精準」,我只要求它「有點準」就好。甚麼是有點準?我可以自己給出一個關於有點準的定義:已知物體的位置被觀測後塌縮後的機率分佈會有些胖胖的,我測出物體落在x1到x2這兩個位置之間的機率有80%,雖然沒有絕對的確定它在x1到x2這之間的哪個位置,但我們給了這個位置的範圍,這個範圍的選取是「機率有80%」,於是我們說這80%即是所謂的「有點準」。
現在,我把物體位置的機率分布做傅立葉轉換,可以得到物體動量的機率分布。我於是可以選取兩個動量值p1和p2,並發現測得的物體動量落在p1和p2之間的機率是80%,因此我們也知道了「有點準」的動量分布範圍。我定義x1和x2的差值叫Δx,p1和p2的差值叫Δp。值得注意的是,可以讓兩個位置之間存在機率等於80%的x1和x2有無限多種,為求統一我需要選取Δx最小的那一種,同樣的動量也是一樣(這種選法解釋了為甚麼大部分不準量都是從機率分佈的峰值向側邊展開)。因此我可以粗略給出Δx和Δp的定義如下:
由剛才給的數學例子不難發現,對任何形式的分布來說,ΔxΔp的大小一定有個下限。因而可以做出以下結論:
在古典物理我們會說,一個物體t時刻後將會有100%的機率存在某一個位置點,代表這個物體的位置是「確定」的,如果能用最尖端的儀器零誤差的把這個位置測出來,那這個位置就被我們給絕對「測準」了。
量子力學告訴我們,位置是機率分佈函數,除非是剛剛提的Dirac delta Function,否則我們不可能預測物體將會100%存在於一個位置點(這部分若還不理解,可以再回顧一下黃衣人和黑衣人的例子),因此準的定義就要做點修改了。讓我們把定義修改成物體t時刻後將會有100%的機率存在於一個位置區間,並將這個區間的寬度稱做不準量。然而,除非你的機率分佈是像之前舉過的方形脈衝這類函數,否則對大部分的機率分佈,這種定義下的不準量寬度將是無限大。
於是為了滿足實務需求,讓我們再重修一次定義:物體t時刻後會有機率P落在一個位置區間,那這個區間可能有的寬度最小值就是相對P這個存在定義下的不準量。為求方便統一,一般物理學家都會將這個P對應到的寬度設定為標準差。當一個位置機率分佈的不準量愈小,則位置就愈能被「確定」在某個區間,所以這個物體的位置機率分佈就「愈準」。當你的機率分布函數愈寬,你就愈難把你可能測到的值「確定」在某個範圍內,因此其實用「不確定性原理」來翻譯會更來的恰當。
最後來看看隱藏在測不準原理背後的數學理論。從最本質來看,互為對偶空間的兩個參數無法同時被測準,就是測不準原理。因此測不準原理並不只適用於位置和動量,例如能量和時間也互為對偶空間,所以兩者一樣滿足測不準關係。至於為甚麼波會有對偶效應,就如同在問為甚麼物體無法超越光速一樣,只能歸咎於大自然的本質,更精確來說它其實是一種數學的本質。事實上在量子力學中,位置和動量都是一種「算子」;廣義來看的話,任何物理量,像是動能、位能、角動量等等,都是「厄米特算子」(Hermitian)。考慮一個算子A,其精確的不準量定義可以由算子對應當下波函數的期望值推算如下:
有了算子,量子矩陣力學中定義了一種叫做對易子(Commutator)的算符,可將兩個算子A和B轉換成下面的型式:
數學上可以推導出一個定理:如果A和B皆為厄米特算子,則它們的不準量乘積必定大於等於其對易子期望值的大小的一半。這個定理被稱做測不準定理。
只要兩個厄米特算子的對易子大小等於零,那這兩個算子對應的物理量就可以同時被測準。動量和位置是厄密特算子,但它們的對易子大小為約化普朗克常數,所以自然沒辦法同時被測準,因而測不準原理其實是一個從數學觀點來看必然的事實。
量子力學有三種繪景(Picture),分別是薛丁格繪景、海森堡繪景和狄拉克繪景,其描述量子力學的方式分別為波動力學、矩陣力學和交互作用。這三種繪景雖然描述量子力學系統採用的觀點不同,但最後所得到的結果都相同。以測不準原理來說,從薛丁格繪景看的話,因為物質有波動性,動量和位置互為對偶空間,所以它們無法同時被測準。從海森堡繪景看的話,則是因為動量和位置在量子力學公設下為厄米特算符,而兩者的對易子不為零,所以無法同時被測準。雖然前者解釋的方式比較直覺,後者比較像數學證明,但其實歸根到底在解釋的現象具備完全一樣的本質。
測不準原理之所以難以理解往往都出在於幾個原因:不了解「準」的意涵、不清楚「觀測行為」的物理意義,以及不知道要怎麼「證明」。做個總結的話,古典力學假設所有物體的波函數都是脈衝函數(Dirac delta Function),所以你可以確定物體的動量和位置。但量子力學表示波函數只要滿足薛丁格方程和邊界條件即可,所以物體可以同時有很多位置和很多動量。「準」代表著波函數胖胖的程度、「觀測行為」代表從外部施加位能來讓薛丁格方程解出來的波函數塌縮到很小的範圍、「證明」則是在量子力學的波函數算子公設下,用波動性或對易原理來解釋。
測不準原理在講的即是:位置波函數和動量波函數的寬度相乘是有下限的,固想同時精確測量兩者的量值將會有其極限。希望看完這篇筆記後,你將不再對測不準原理感到困惑。
現在讓我給一個思想實驗來加深對測不準原理的理解。假想有1000萬個一樣的盒子,每個盒子裡面都裝著一模一樣的物體。每個盒子旁各站一個人,在同一個時間讓這1000萬個人把面前的盒子打開,並且「測量」他們所看到的「物體位置」。這邊先假設這些人測量位置的技術能達到完美,晚點再討論不完美的情況。
因為物體的位置在盒子被打開前僅是一種機率分布,所以即使初始條件相同(一樣的盒子,一樣的物體,同時打開),打開盒子後每個人看到的物體的位置都不太一樣:假設看到物體位於x1的人有a1個,物體位於x2的人有a2個......依此類推,接著我們可以做出一張分布圖,橫軸是物體的位置x,縱軸是看到物體位在x的人數a,當我們把1000萬人推廣到無限人,這張分布圖便是物體的位置機率分佈。
用相同的方法,如果我們在讓這1000萬個人把面前的盒子打開的同時,請他們「測量」的是他們所看到的「物體動量」,便可以得到物體的動量機率分佈。最神奇的事情發生了:你將會發現,這兩個機率分佈的原波函數互為對方的傅立葉變換。量子力學是正確的!

「觀測」在整個過程中扮演的角色是:當你在想辦法「測量位置」時,可以等效於你給系統施加了一個位能,把這個位能丟進薛丁格方程式去解,得到的波函數會變得尖尖的,看起來就很像波函數塌縮到一個點上,這個過程又被稱作量子塌縮。如果你的測量位置的方法達到完美時,塌縮後的波函數會尖到變成Dirac delta Function,換句話說你可以宣稱你確定了物體的位置。但如果你的測量能力沒有那麼好,得到的波函數就會不會那麼尖,可能會變成一個有點胖的高斯函數。
基於測不準原理的限制,當你完美測量位置時,動量不準量就會變無限大。同樣的,當你完美去測量動量時,位置的不准量就會變無限大。你可能會想,如果我今天安排兩組人站在盒子旁,這邊稱作黃衣人和黑衣人。當盒子打開時,黃衣人測裡面物體的位置,黑衣人測裡面物體的動量,這樣裡面那個物體的位置和動量不就同時被確定了嗎,哪來的測不準?
基於測不準原理的限制,當你完美測量位置時,動量不準量就會變無限大。同樣的,當你完美去測量動量時,位置的不准量就會變無限大。你可能會想,如果我今天安排兩組人站在盒子旁,這邊稱作黃衣人和黑衣人。當盒子打開時,黃衣人測裡面物體的位置,黑衣人測裡面物體的動量,這樣裡面那個物體的位置和動量不就同時被確定了嗎,哪來的測不準?
事實上這個時候,你的等效外加位能包含了「黃衣人測量位置的外加位能」與「黑衣人測量動量的外加位能」,因此把這兩個位能疊加後考慮進薛丁格方程裡頭,最後得到的波函數就無法在動量和位置上都成為Dirac delta Function,而是都有些胖胖的,不準量分別是Δx和Δp,物體在此時就會同時擁有很多位置和很多動量。如果Δx和Δp很小的話,一般人肉眼分辨不出這些不同位置及不同動量的微小差異,因而會自動把位置波函數和動量波函數的期望值看作是位置和動量的精確值。但如果Δx和Δp很大的話,你所看到的物體位置可能就會變得糊成一團、物體動量則好像同時用一堆不同方向不同大小的速度晃動,這就是許多量子力學科普書很愛描述的量子微觀現象。
關於測不準原理物理意義的詮釋就到這邊,我要回過頭來給出一個波函數「準」的程度的數學定義。回到高斯機率分佈函數的例子:我不要求位置的測量「絕對精準」,我只要求它「有點準」就好。甚麼是有點準?我可以自己給出一個關於有點準的定義:已知物體的位置被觀測後塌縮後的機率分佈會有些胖胖的,我測出物體落在x1到x2這兩個位置之間的機率有80%,雖然沒有絕對的確定它在x1到x2這之間的哪個位置,但我們給了這個位置的範圍,這個範圍的選取是「機率有80%」,於是我們說這80%即是所謂的「有點準」。
現在,我把物體位置的機率分布做傅立葉轉換,可以得到物體動量的機率分布。我於是可以選取兩個動量值p1和p2,並發現測得的物體動量落在p1和p2之間的機率是80%,因此我們也知道了「有點準」的動量分布範圍。我定義x1和x2的差值叫Δx,p1和p2的差值叫Δp。值得注意的是,可以讓兩個位置之間存在機率等於80%的x1和x2有無限多種,為求統一我需要選取Δx最小的那一種,同樣的動量也是一樣(這種選法解釋了為甚麼大部分不準量都是從機率分佈的峰值向側邊展開)。因此我可以粗略給出Δx和Δp的定義如下:
由剛才給的數學例子不難發現,對任何形式的分布來說,ΔxΔp的大小一定有個下限。因而可以做出以下結論:
在古典物理我們會說,一個物體t時刻後將會有100%的機率存在某一個位置點,代表這個物體的位置是「確定」的,如果能用最尖端的儀器零誤差的把這個位置測出來,那這個位置就被我們給絕對「測準」了。
量子力學告訴我們,位置是機率分佈函數,除非是剛剛提的Dirac delta Function,否則我們不可能預測物體將會100%存在於一個位置點(這部分若還不理解,可以再回顧一下黃衣人和黑衣人的例子),因此準的定義就要做點修改了。讓我們把定義修改成物體t時刻後將會有100%的機率存在於一個位置區間,並將這個區間的寬度稱做不準量。然而,除非你的機率分佈是像之前舉過的方形脈衝這類函數,否則對大部分的機率分佈,這種定義下的不準量寬度將是無限大。
於是為了滿足實務需求,讓我們再重修一次定義:物體t時刻後會有機率P落在一個位置區間,那這個區間可能有的寬度最小值就是相對P這個存在定義下的不準量。為求方便統一,一般物理學家都會將這個P對應到的寬度設定為標準差。當一個位置機率分佈的不準量愈小,則位置就愈能被「確定」在某個區間,所以這個物體的位置機率分佈就「愈準」。當你的機率分布函數愈寬,你就愈難把你可能測到的值「確定」在某個範圍內,因此其實用「不確定性原理」來翻譯會更來的恰當。
最後來看看隱藏在測不準原理背後的數學理論。從最本質來看,互為對偶空間的兩個參數無法同時被測準,就是測不準原理。因此測不準原理並不只適用於位置和動量,例如能量和時間也互為對偶空間,所以兩者一樣滿足測不準關係。至於為甚麼波會有對偶效應,就如同在問為甚麼物體無法超越光速一樣,只能歸咎於大自然的本質,更精確來說它其實是一種數學的本質。事實上在量子力學中,位置和動量都是一種「算子」;廣義來看的話,任何物理量,像是動能、位能、角動量等等,都是「厄米特算子」(Hermitian)。考慮一個算子A,其精確的不準量定義可以由算子對應當下波函數的期望值推算如下:
數學上可以推導出一個定理:如果A和B皆為厄米特算子,則它們的不準量乘積必定大於等於其對易子期望值的大小的一半。這個定理被稱做測不準定理。
只要兩個厄米特算子的對易子大小等於零,那這兩個算子對應的物理量就可以同時被測準。動量和位置是厄密特算子,但它們的對易子大小為約化普朗克常數,所以自然沒辦法同時被測準,因而測不準原理其實是一個從數學觀點來看必然的事實。
量子力學有三種繪景(Picture),分別是薛丁格繪景、海森堡繪景和狄拉克繪景,其描述量子力學的方式分別為波動力學、矩陣力學和交互作用。這三種繪景雖然描述量子力學系統採用的觀點不同,但最後所得到的結果都相同。以測不準原理來說,從薛丁格繪景看的話,因為物質有波動性,動量和位置互為對偶空間,所以它們無法同時被測準。從海森堡繪景看的話,則是因為動量和位置在量子力學公設下為厄米特算符,而兩者的對易子不為零,所以無法同時被測準。雖然前者解釋的方式比較直覺,後者比較像數學證明,但其實歸根到底在解釋的現象具備完全一樣的本質。
測不準原理之所以難以理解往往都出在於幾個原因:不了解「準」的意涵、不清楚「觀測行為」的物理意義,以及不知道要怎麼「證明」。做個總結的話,古典力學假設所有物體的波函數都是脈衝函數(Dirac delta Function),所以你可以確定物體的動量和位置。但量子力學表示波函數只要滿足薛丁格方程和邊界條件即可,所以物體可以同時有很多位置和很多動量。「準」代表著波函數胖胖的程度、「觀測行為」代表從外部施加位能來讓薛丁格方程解出來的波函數塌縮到很小的範圍、「證明」則是在量子力學的波函數算子公設下,用波動性或對易原理來解釋。
測不準原理在講的即是:位置波函數和動量波函數的寬度相乘是有下限的,固想同時精確測量兩者的量值將會有其極限。希望看完這篇筆記後,你將不再對測不準原理感到困惑。
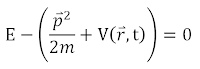
















This comment has been removed by the author.
ReplyDelete第一個問題我讀的不是很懂(雲霧室、定量?),可能得請你再解釋清楚一點你想問什麼 :)
Delete第二個問題,我的理解是這樣的:決定物體位置確定性的是它所處的位能,而不是觀測者眨眼的動作。所以如果這個位能沒辦法讓這個物體的不準量低到一定的範圍內的話,那麼在你視線中,它就會同時存在多處,所以看起來是「糊的」,。
This comment has been removed by the author.
Delete我的觀點是,別去想什麼「移除測量」、「下次測量」。測量就是施加新的位能,所以我覺得應該關注的,是「你現在的位能條件,會給你的波函數帶來多大的不準量?」,以及「隨著位能變化,波函數的不準量會怎麼改變?」這兩件事情。
Delete在「測量就是施加新的位能」的這個想法下,觀測就不一定會讓波函數塌縮成 Dirac delta function 了。波函數要塌縮成 Dirac delta function,前提是你在觀測時所施加的位能,在計算後,剛好能讓波函數的不準量逼近零。但如果不行的話,就會造成你在第二點裡困惑的「看起來存在多個位置」的現象。
至於在雙狹縫實驗裡頭,顯示的位置是確定的結果,我認為是因為這個實驗的「觀測行為」所施加的位能,能讓波函數的位置不準量逼近零。
而你提到的「不準度應該是來自對每個獨立的電子的測量結果的偏差的計算」,這是因為在這個例子裡,波函數會塌縮,而它在不同點塌縮的機率不一樣,在統計上可以用結果回推原本波函數的樣貌,進而算出它原本的不準量。但這並不代表一個被觀測的波函數,位置不準量一定要是零。
當然以上這些是我自己的理解,量子力學有很多奇怪的地方,我也不敢保證我的看法一定是對的。
This comment has been removed by the author.
Delete我覺得是這樣沒錯。
Delete最後必須強調一下,「測量就是施加新的位能」這件事純粹是我的理解,我沒辦法百分之百有把握的跟你說這個理解方式一定是正確。主要是因為過去在查波函數塌縮的資料時,得到的都是一些模糊不清的解釋,我問不同的教授也得到不同的說法,感覺這東西在學界爭論也蠻大的。
而我在整理當時所知的資訊時,覺得自己比較能接受這個解釋方法,所以在這篇裡頭就把它當作我的基本假設。原本計畫大三大四把它弄的更清楚,但因為我後來跑去讀數學,然後又接著休學,這塊就沒什麼時間碰了 Orz
如果你有認識的量子力學高手提出更有說服力的解釋,非常歡迎你把它提出來,哈哈 XD
This comment has been removed by the author.
Delete